Trigonometri (cosinus, sinus, tangen)

A. Pengertian

Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.

B. Penggunaan Rumus Sinus dan Cosinus Jumlah Dua Sudut, Selisih Dua Sudut, dan Sudut Ganda

1. Rumus Cosinus Jumlah dan Selisih Dua SudutSebelum membahas rumus trigonometri cosinus untuk jumlah dan selisih dua sudut, perlu kamu ingat kembali dalam segitiga siku-siku ABC berlaku: 

Selanjutnya, perhatikanlah gambar berikut.

Dari lingkaran yang berpusat di O(0, 0) dan berjari-jari 1 satuan misalnya,

∠ AOB = ∠ A

∠ BOC = ∠ B

maka ∠AOC = ∠ A + ∠ B

Dengan mengingat kembali tentang koordinat

Cartesius, maka:

a. koordinat titik A (1, 0)

b. koordinat titik B (cos A, sin A)

c. koordinat titik C {cos (A + B), sin (A + B)}

d. koordinat titik D {cos (–B), sin (–B)} atau (cos B, –sin B)

(α + β), yaitu

cos(α – β)= cos (α + (–β))

= cos α cos(–β) – sin α sin(–β)

= cos α cos β + sin α sin β

cos (α – β) = cos α cos β + sin α sin β

2. Rumus Sinus Jumlah dan Selisih Dua Sudut

Perhatikan rumus berikut ini.

Maka rumus sinus jumlah dua sudut: sin (A + B) = sin A cos B + cos A sin B

Dengan cara yang sama, maka:

sin (A – B) = sin {A + (–B)}

= sin A cos (–B) + cos A sin (–B)

= sin A cos B – cos A sin B

Rumus sinus selisih dua sudut: sin (A – B) = sin A cos B – cos A sin B

3. Rumus Tangen Jumlah dan Selisih Dua Sudut

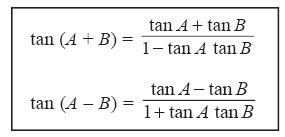
4. Penggunaan Rumus Sinus, Cosinus, dan Tangen Sudut Ganda

Rumus untuk sin 2α

Anda telah mengetahui bahwa

sin (α + β) = sin α cos β + cos α sin β.

Untuk β = α, diperoleh

sin (α + α) = sin α cos α + cos α sin α

sin 2 α = 2 sin α cos α

Jadi, sin 2α = 2 sin α cos α

Rumus untuk cos 2α

Anda juga telah mempelajari bahwa

Rumus untuk tan 2α

Perkalian, Penjumlahan, serta Pengurangan Sinus dan Kosinus

Perkalian Sinus dan Kosinus

Kita telah mempelajari rumus-rumus jumlah dan selisih dua sudut dalam trigonometri, yaitu:

Penjumlahan dan Pengurangan Sinus

Rumus perkalian sinus dan kosinus dalam trigonometri di bagian C.1 dapat

ditulis dalam rumus berikut.

Identitas Trigonometri

Contoh Soal Trigonometri

Sumber :

1. http://matematika-ipa.com/trigonometri-rumus-trigonometri/

2. Mahir Mengembangkan Kemampuan Matematika untuk Kelas XI Program Ilmu Pengetahuan Alam